Schottky group

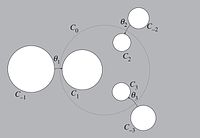
Okay, imagine that you and your friends are playing a game. In this game, you can only move in certain directions and you have to stay within certain boundaries. This is kind of like a map that tells you where you can go and where you can't go.

But there's a twist – you can also reflect your movements off of certain lines on the map! So if you were about to move off the edge of the map, you could instead bounce back off of the boundary and move in a different direction.

This is kind of like how a Schottky group works. It's a group of transformations – like rotations, reflections, and translations – that operate within a certain space. But these transformations are also allowed to reflect off of certain boundary lines in that space.

This might sound complicated, but it's actually really helpful for mathematicians who study geometric shapes and spaces. By using Schottky groups, they can explore the different ways that something like a sphere or a plane can be transformed without changing its overall shape or structure.

So in short, a Schottky group is a special kind of group that lets you make certain transformations within a certain space, and then reflect those transformations off of certain boundary lines in that space. It's like a game where you have to follow certain rules, but you can also bounce off walls and keep going in different directions.