Total variation distance

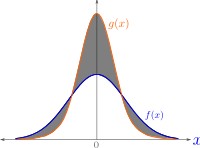
Total variation distance is a way to measure how different two things are. It's like the distance between you and your friend when you're playing a game of tag. The farther apart you are, the harder it is for you to tag them. Similarly, the greater the total variation distance between two things, the more different they are from each other.

For example, let's say you have two bags of candy. Bag A has 5 red and 5 blue candies, while bag B has 9 red and 1 blue candy. To calculate the total variation distance between the two bags, you need to find the absolute difference in the number of red and blue candies in each bag, and add them up.

In bag A, there is a difference of 5 between the number of red and blue candies. In bag B, there is a difference of 8 between the number of red and blue candies. Adding these two differences together gives us a total variation distance of 13.

This means that the two bags of candy are quite different from each other, and it might be hard to mistake one for the other. On the other hand, if the two bags had a total variation distance of 0, it would mean that they are exactly the same and you wouldn't be able to tell them apart.

Total variation distance is used in many different areas, like statistics, probability, and cryptography, to compare different data sets and measure how similar or different they are.