Homological algebra

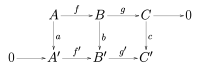
Homological algebra is the science of studying shapes and spaces by breaking them down into small, manageable pieces and then putting them back together like a puzzle.

Imagine you have a big box with lots of different shapes inside, like triangles, circles, and squares. Homological algebra helps you understand how those shapes fit together and how to rearrange them in different ways.

First, imagine you take one of the shapes out of the box and examine it more closely. You might notice that it has some sides and angles that are important for determining how it fits together with the other shapes. These are called its "features."

Now imagine you take out another shape and look at its features. You might notice that some of the features are similar to the first shape, while others are different. This is important because it shows you how the two shapes can fit together.

Homological algebra takes all of these features into account and uses them to create a kind of "map" of how the shapes fit together. This map is called a "complex" and it helps you visualize how different parts of the shape are connected.

Using homological algebra, you can study different types of shapes and spaces and figure out how they fit together. It's a bit like being a detective, piecing together clues to solve a mystery. But instead of solving a crime, you're understanding the mysteries of the universe!