Hypergeometric distribution
Imagine you have a big bag of colored marbles and you want to know the chances of picking a certain number of marbles of a certain color without looking.
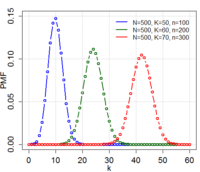
The hypergeometric distribution helps us figure that out. We use it when we have a fixed number of total objects in a group, and we want to know the probability of getting a certain number of specific objects from that group when we randomly pick another fixed number of objects without replacement.
So let's look at that bag of marbles. Say we have 20 marbles total, with 10 blue and 10 red. If we want to know the chances of picking 3 blue marbles out of 5 picks, we would use the hypergeometric distribution.
The hypergeometric distribution takes into account the total number of objects, the number of "success" objects (in this case, blue marbles), the number of "failure" objects (red marbles), and the number of picks we are making.
Using the formula, we can calculate the probability of picking 3 blue marbles out of 5 picks from the bag of 20 marbles. The answer is 0.2551, or about a 25.5% chance of getting 3 blue marbles out of 5 picks.
The hypergeometric distribution comes in handy for many things, like figuring out the probability of drawing a certain number of aces from a deck of cards or the likelihood of a certain number of defective items in a batch of production.
The hypergeometric distribution helps us figure that out. We use it when we have a fixed number of total objects in a group, and we want to know the probability of getting a certain number of specific objects from that group when we randomly pick another fixed number of objects without replacement.
So let's look at that bag of marbles. Say we have 20 marbles total, with 10 blue and 10 red. If we want to know the chances of picking 3 blue marbles out of 5 picks, we would use the hypergeometric distribution.
The hypergeometric distribution takes into account the total number of objects, the number of "success" objects (in this case, blue marbles), the number of "failure" objects (red marbles), and the number of picks we are making.
Using the formula, we can calculate the probability of picking 3 blue marbles out of 5 picks from the bag of 20 marbles. The answer is 0.2551, or about a 25.5% chance of getting 3 blue marbles out of 5 picks.
The hypergeometric distribution comes in handy for many things, like figuring out the probability of drawing a certain number of aces from a deck of cards or the likelihood of a certain number of defective items in a batch of production.
Related topics others have asked about:
