Inner product space
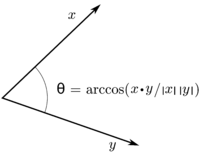
An inner product space is like a special kind of space where we can measure angles and distances between things, like lines or vectors.
Imagine you have a toy airplane on a table. You can tell that it's pointing to the right, and maybe it's tilted a bit up or down. You can turn it and change its position, and it can move all around the table.
Now, imagine you have another toy airplane, and you want to know how much one is pointing towards the other. You could try to compare where they're pointing, but that might not give you a precise answer. Instead, you could use an inner product to tell you how much one toy airplane is pointing towards the other.
An inner product is like a rule that describes how much two things "match" each other. In an inner product space, we have two special operations we can do with vectors:
- We can add vectors together. This means we can combine two vectors into one, like adding the toy airplane's position and its direction.
- We can multiply vectors together using the inner product. This lets us compare two vectors and see how "in line" they are with each other.
For example, let's say we have two vectors on a line, like a toy car moving forwards and backwards. We can use the inner product to see how much the car is pointing towards a specific direction, like a finish line. The inner product tells us how much the vectors "match" - if they're pointing in exactly the same direction, the inner product is one. If they're pointing in opposite directions, the inner product is negative one. If they're at a 90 degree angle, the inner product is zero.
Overall, an inner product space is a place where we can use inner products to compare different vectors and see how much they match. This can be really helpful in lots of different areas of math and science!
Imagine you have a toy airplane on a table. You can tell that it's pointing to the right, and maybe it's tilted a bit up or down. You can turn it and change its position, and it can move all around the table.
Now, imagine you have another toy airplane, and you want to know how much one is pointing towards the other. You could try to compare where they're pointing, but that might not give you a precise answer. Instead, you could use an inner product to tell you how much one toy airplane is pointing towards the other.
An inner product is like a rule that describes how much two things "match" each other. In an inner product space, we have two special operations we can do with vectors:
- We can add vectors together. This means we can combine two vectors into one, like adding the toy airplane's position and its direction.
- We can multiply vectors together using the inner product. This lets us compare two vectors and see how "in line" they are with each other.
For example, let's say we have two vectors on a line, like a toy car moving forwards and backwards. We can use the inner product to see how much the car is pointing towards a specific direction, like a finish line. The inner product tells us how much the vectors "match" - if they're pointing in exactly the same direction, the inner product is one. If they're pointing in opposite directions, the inner product is negative one. If they're at a 90 degree angle, the inner product is zero.
Overall, an inner product space is a place where we can use inner products to compare different vectors and see how much they match. This can be really helpful in lots of different areas of math and science!
Related topics others have asked about:
