Numerical differentiation

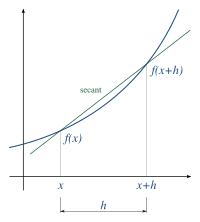
Numerical differentiation is a way to find out how fast something is changing by using math and numbers. Think of it like measuring how fast your toy car is going or how steep a hill is.

Let's say you have a graph that shows how a toy car is moving over time. You want to know how fast it's going at a certain point on the graph. But you don't have a fancy speedometer to measure it. So what do you do?

You can use numerical differentiation to calculate the car's speed at that point. This means you look at how much the car has moved over a certain amount of time and use that to estimate its speed.

But how do you do that exactly? Well, you take two points on the graph that are very close to each other (like two dots that are next to each other). Then, you draw a straight line that goes through those two points. The slope of that line (how steep it is) will tell you how fast the car is going at that point in time.

That's basically what numerical differentiation does - it calculates the slope of a line between two points on a graph to estimate how fast something is changing (like the car's speed). It's not always perfect, but it's a good way to get a rough idea of what's going on.