Extended real number line

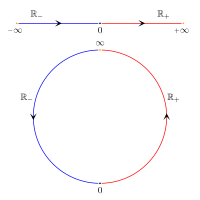
Imagine you have a bunch of numbers, like 1, 2, 3, and so on. These are all real numbers that you are probably familiar with. But what if you also want to talk about numbers like infinity or negative infinity? That's where the extended real number line comes in.

The extended real number line is like a regular number line, but it has two special points at either end: positive infinity and negative infinity. These points represent numbers that are really, really big (positive infinity) or really, really small (negative infinity).

Now, you might be wondering how we can add or subtract infinity from other numbers. Well, we can't! In math, infinity is not really a number in the usual sense. Instead, it's more of an idea or a concept. So when we talk about adding or subtracting infinity, we're really just talking about a limit or an approximation.

For example, if you add a really large number to infinity, you might get infinity again. But if you add a really small positive number to negative infinity, you might get a slightly less negative number. Similarly, if you subtract a really small positive number from infinity, you might get a slightly smaller infinity.

So why do we need the extended real number line? Well, it helps us talk about certain mathematical concepts that involve infinity, like limits and continuity. Plus, it's just a handy way to visualize numbers that are really big or really small.